힙(Heap)이란?
힙이란 완전 이진 트리의 일종으로, 여러 개의 값들 중 최댓값이나 최솟값을 빠르게 찾아내도록 만들어진 자료구조이다.
힙은 트리의 루트 노드에 데이터들의 최댓값 또는 최솟값을 저장한다.
즉, 부모 노드의 키 값이 자식 노드의 키 값보다 항상 큰(작은) 이진 트리를 말한다.
최대 힙 & 최소 힙
최대 힙 (max heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 크거나 같은 이진 트리
- 루트 노드에 힙의 최댓값 저장
최소 힙 (min heap)
- 부모 노드의 키 값이 자식 노드의 키 값보다 작거나 같은 이진 트리
- 루트 노드에 힙의 최솟값 저장

힙의 삽입
다음의 과정을 거쳐서 힙에 데이터를 삽입한다.
1. 힙의 가장 마지막에 데이터를 삽입한다.
2. 삽입한 노드의 부모 노드와 키 값을 비교하여 조건에 만족하지 않는다면 두 노드의 위치를 바꾼다.
(이때 조건은 부모 노드의 키 값이 더 큰(작은) 것을 말한다)
3. 힙의 성질을 만족할 때까지 2번을 반복한다.
예시
아래 최대 힙에 `7`을 삽입하는 예시를 보자.

1. 힙의 마지막에 `7`을 삽입한다.
최대 힙이므로 부모 노드의 키 값은 자식 노드의 키 값보다 항상 커야 한다.

2. `7`의 부모 노드와 키 값을 비교했을 때 7의 값이 더 크므로 두 노드의 위치를 바꾼다.
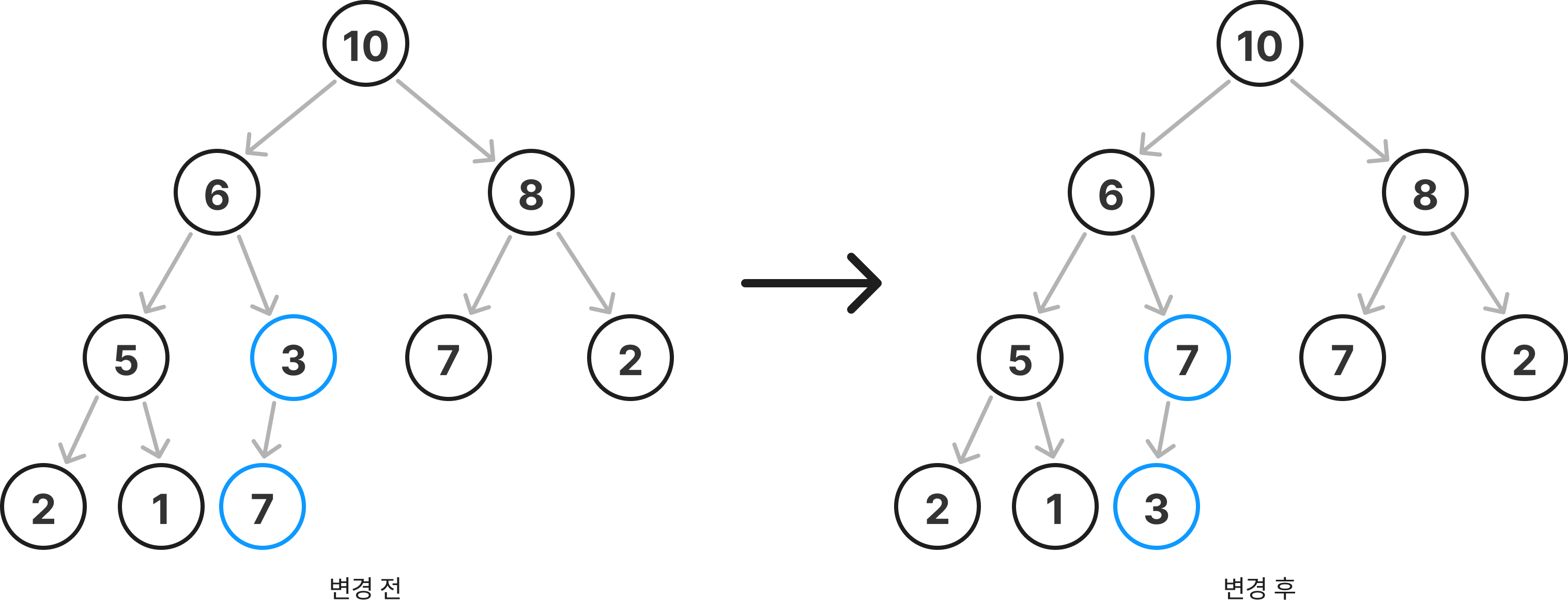
3. 삽입한 데이터인 `7`과 부모 노드인 `6`을 비교했을 때 부모 노드의 키 값이 더 작으므로 마찬가지로 두 노드의 위치를 바꾼다.

4. 다시 부모 노드와 비교를 했을 때, 이번엔 부모 노드가 더 크므로 끝낸다.

힙의 삭제
다음의 과정을 거쳐서 힙의 최댓값 또는 최솟값을 삭제한다.
1. 힙의 루트 노드를 삭제한다.
2. 힙의 가장 마지막에 있는 노드를 루트 노드로 가져온다.
3. 루트 노드로 가져온 노드의 값과 그 자식 값을 비교하여 힙의 성질을 만족할 때까지 두 노드의 위치를 바꾼다.
예시
위에서 사용한 최대 힙을 `pop()` 하는 예시를 보자.

1. 트리의 루트 노드 10을 삭제하며 반환한다.

2. 가장 마지막에 있던 노드인 `1`을 루트로 가져온다.
이제 최대 힙의 성질이 깨졌기 때문에 재조정이 필요하다.

3. 루트 노드의 자식 노드들과 비교하여 더 큰 노드가 위로 오도록 `swap`을 해준다.
`1`의 자식 노드인 `6`과 `8` 중 `8`이 더 크므로 `8`과 `1`을 `swap` 한다.

4. 3번과 마찬가지로 `1`과 자식 노드들을 비교하여 더 큰 값을 찾는데 그 중 더 큰 값인 `7`과 `swap`한다.

5. 더 이상 자식 노드가 없으므로 끝낸다.

이렇게 하면 최대 힙의 성질을 유지하며 데이터를 삽입하고 삭제할 수 있다!
이 글을 쓰다가 한 번 글이 완전 날아가버려서.. 조금 의욕이 떨어진 채로 썼다는 tmi~ 와 함께 글을 마칩니다 ⎝⍢⎠